This is a brief tutorial on implementing loop convergence proofs in KeYmaera X. I’ll assume you already know all about loop variants and just want to get started using this proof technique in KeYmaera X / dynamic logic.

I’ll use a very simple theorem as the running example:

x < 0 -> <{x:=x+1;}*>x>0

Intuitively, the formula states that if x<0 initially, then after repeating x := x + 1 some number of times, we find a state where x>0.

Proving this property requires finding a loop variant j(v) and using this variant together with the loop convergence proof rule:

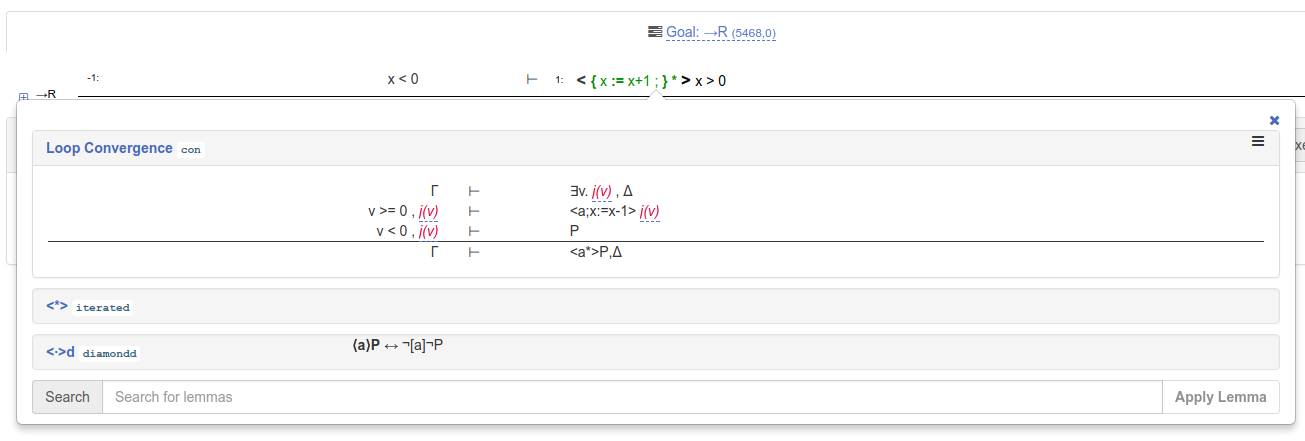
The Loop Convergence proof rule in differential dynamic logic

For this model, the loop variant x = -v + 1 is sufficient. To use the proof rule with this loop variant, click on the web form and enter the variant in the web form. You might get a warning message:

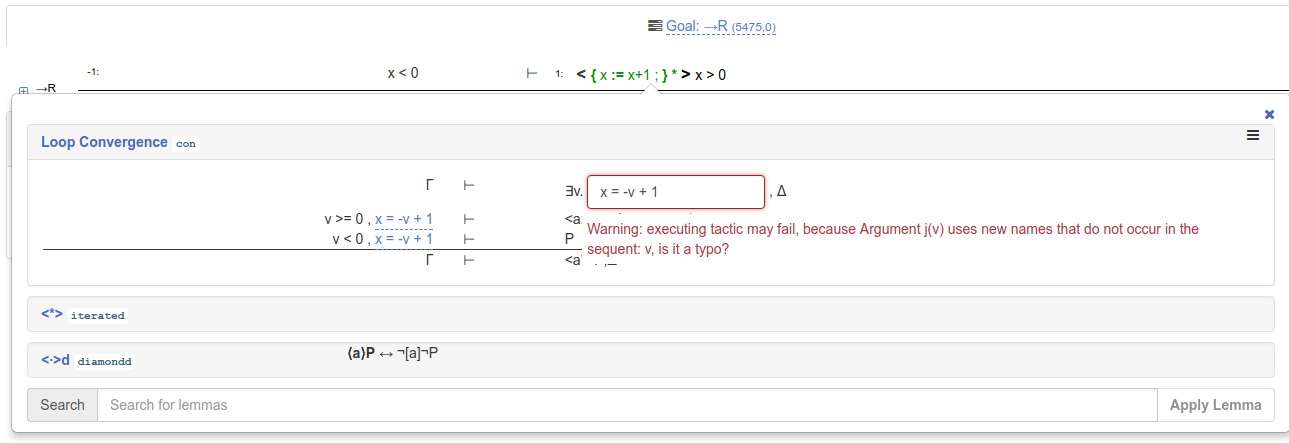
The Loop Convergence proof rule in differential dynamic logic -- warning message

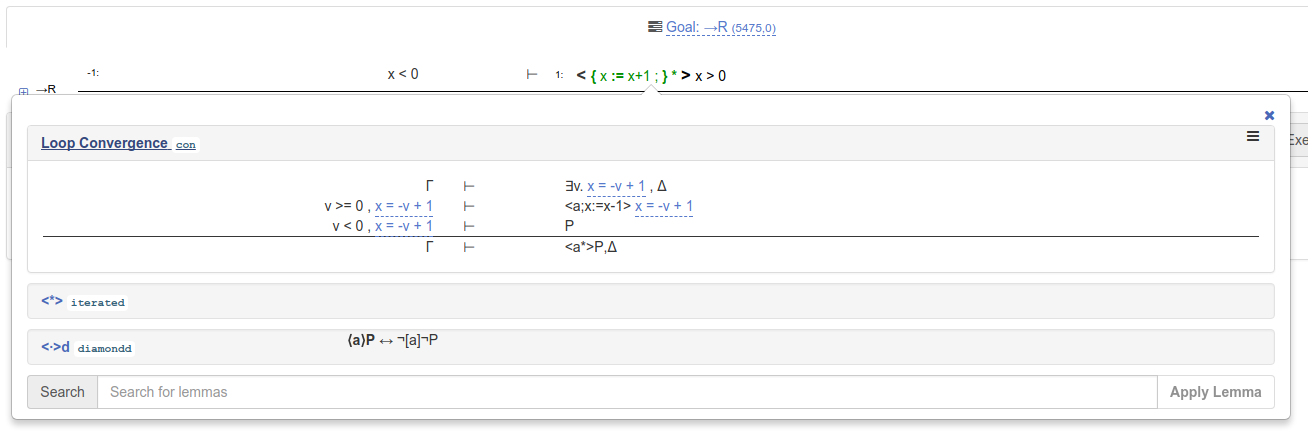
You can ignore this warning message by clicking anywhere outside of the warning message box. Then, click on the proof rule to execute the loop convergence proof step:

The Loop Convergence proof rule in differential dynamic logic -- ignoring the warning message

Alternatively, you can simply type the

con({`x=-v+1`}, 1)

tactic into the tactic editor box:

The Loop Convergence proof rule in differential dynamic logic -- using con({`j(v)`}, 1) from the tactic editor

You’ll now have three goals, two of which are arithmetic and one of which requires a single application of assignd (diamond assign axiom) before cosing.

The final tactic:

implyR(1) ; con({`x=-v+1`}, 1) ; <(
  QE
  ,
  assignd(1) ; QE
  ,
  QE
)

More Resources